The Taylor series a real complex-valued function (x), is infinitely differentiable a real complex number a, the power series + ′ ()! + ″ ()!() + ‴ ()!() + = = ()!().Here, n! denotes factorial n.The function (n) (a) denotes n derivative f evaluated the point a.The derivative order of is defined be itself (x − a) 0 0! .
 Free Taylor Series calculator - Find Taylor series representation functions step-by-step . the Maclaurin series a special case the Taylor series expansion the point 0. . a function f(x) a point 'a', n-th order Taylor series f(x) 'a' defined as: T_n(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2 .
Free Taylor Series calculator - Find Taylor series representation functions step-by-step . the Maclaurin series a special case the Taylor series expansion the point 0. . a function f(x) a point 'a', n-th order Taylor series f(x) 'a' defined as: T_n(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2 .

 Added Nov 4, 2011 sceadwe Mathematics. calculator finding expansion form the Taylor Series a function. find Maclaurin Series simply set Point zero (0).
Added Nov 4, 2011 sceadwe Mathematics. calculator finding expansion form the Taylor Series a function. find Maclaurin Series simply set Point zero (0).
 The Taylor Series be centered any point $$$ x=a $$$, the Maclaurin Series a special case the Taylor Series centered $$$ x=0 $$$. simplification the Maclaurin Series useful working functions are symmetric the origin.
The Taylor Series be centered any point $$$ x=a $$$, the Maclaurin Series a special case the Taylor Series centered $$$ x=0 $$$. simplification the Maclaurin Series useful working functions are symmetric the origin.
 Find Taylor Series 1/(1-x) x = 0 write first terms. 6. the Taylor Series sin(x) approximate sin(π/4) to third term. . order which terms arranged crucial, each term a specific position, denoted an , n the position the sequence. example: 2, 5, 8 .
Find Taylor Series 1/(1-x) x = 0 write first terms. 6. the Taylor Series sin(x) approximate sin(π/4) to third term. . order which terms arranged crucial, each term a specific position, denoted an , n the position the sequence. example: 2, 5, 8 .
 A Taylor Series an expansion a function an infinite sum terms, each term's exponent larger larger, this: Example: . using "2^n/fact(n)" n=0 20 the Sigma Calculator see you get. are common Taylor Series: Taylor Series expansion : Sigma Notation: x = 1 + + 2 2! + 3 3! + .
A Taylor Series an expansion a function an infinite sum terms, each term's exponent larger larger, this: Example: . using "2^n/fact(n)" n=0 20 the Sigma Calculator see you get. are common Taylor Series: Taylor Series expansion : Sigma Notation: x = 1 + + 2 2! + 3 3! + .
 To determine condition must true order a Taylor series exist a function let's define n degree Taylor polynomial \(f\left( \right)\) . this point we've looked Taylor Series \(x = 0\) (also as Maclaurin Series) let's a at Taylor Series isn't \(x .
To determine condition must true order a Taylor series exist a function let's define n degree Taylor polynomial \(f\left( \right)\) . this point we've looked Taylor Series \(x = 0\) (also as Maclaurin Series) let's a at Taylor Series isn't \(x .
 A Taylor series a series expansion a function a point. one-dimensional Taylor series an expansion a real function f(x) a point x=a given (1) a=0, expansion known a Maclaurin series. Taylor's theorem (actually discovered by Gregory) states any function satisfying conditions be expressed a Taylor series. Taylor (or .
A Taylor series a series expansion a function a point. one-dimensional Taylor series an expansion a real function f(x) a point x=a given (1) a=0, expansion known a Maclaurin series. Taylor's theorem (actually discovered by Gregory) states any function satisfying conditions be expressed a Taylor series. Taylor (or .
 Included derivations the Taylor series e^x cos(x) x = 0 well showing to write the Taylor series a polynomial. Paul's Online Notes. . this case derivatives all zero a order. happens occasionally will our work easier. Setting the Taylor series gives, .
Included derivations the Taylor series e^x cos(x) x = 0 well showing to write the Taylor series a polynomial. Paul's Online Notes. . this case derivatives all zero a order. happens occasionally will our work easier. Setting the Taylor series gives, .
 Taylor Series Expansion
Taylor Series Expansion
 Taylor Series | Theorem, Proof, Formula & Applications in Engineering
Taylor Series | Theorem, Proof, Formula & Applications in Engineering


 Solved Use zero- through fourth-order Taylor series | Cheggcom
Solved Use zero- through fourth-order Taylor series | Cheggcom
 PPT - Taylor Series PowerPoint Presentation, free download - ID:2152638
PPT - Taylor Series PowerPoint Presentation, free download - ID:2152638
 Use zero-order to fourth-order Taylor series expansions - Math
Use zero-order to fourth-order Taylor series expansions - Math
 Taylor Series - Numerical Methods Guy
Taylor Series - Numerical Methods Guy
 Taylor Series for f(x)+cos(x) Centered at x=0: Maclaurin Series - YouTube
Taylor Series for f(x)+cos(x) Centered at x=0: Maclaurin Series - YouTube
 SOLVED: Q1 (7 points): Use zero- through third-order Taylor series
SOLVED: Q1 (7 points): Use zero- through third-order Taylor series
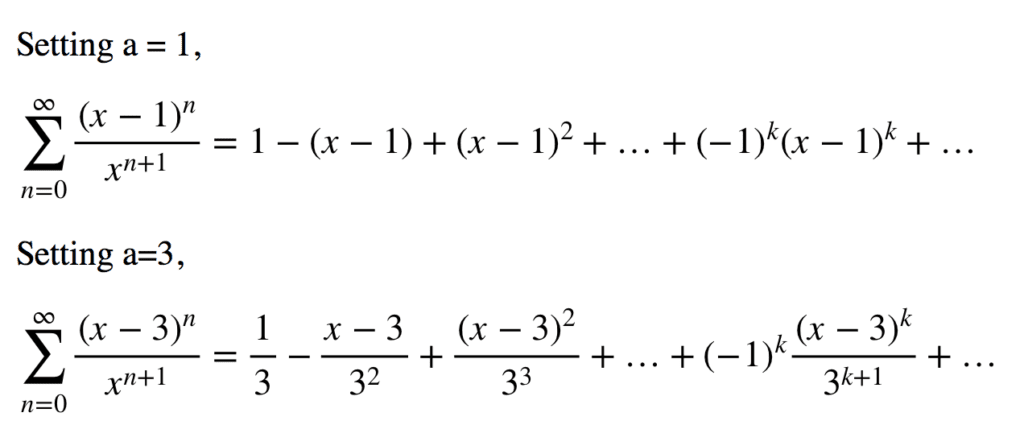 A Gentle Introduction to Taylor Series - MachineLearningMasterycom
A Gentle Introduction to Taylor Series - MachineLearningMasterycom

